
数理物理学
相対性理論、ブラックホール物理学、宇宙物理学、非線形物理学
高次元ブラックホールで新しい物理学の扉を開く
研究背景
近年、AdS/CFT対応を通して、高次元ブラックホールが超電導や超流動などの凝縮系物理学やクオーク・グルーオンプラズマなどの原子物理学の現象を記述することが明らかになってきた。そのため、一見、無関係に思えるブラックホール物理学が、量子論ではアプローチの難しい物性物理学の問題を解決したり、新しい量子物理現象を予言したりすることができるかもしれないと期待されている。このような意味で高次元ブラックホールは、実際に存在するかどうかは別にして、現代物理学において重要な地位を築いている。
研究テーマと成果
アインシュタイン方程式や超重力理論のブラックホールの厳密解の構成を基礎として、アインシュタイン方程式の可積分系の数理構造について研究を行っている。これまでのブラックホールに関する多くの研究では、解析的に簡単であることや解を求めやすいという理由から、コンパクト化されていない漸近平坦なブラックホールに焦点が当てられていたため、コンパクト化されたブラックホール解の新たな生成法を構築し、その手法を用いて、多くのブラックホール解を発見した。
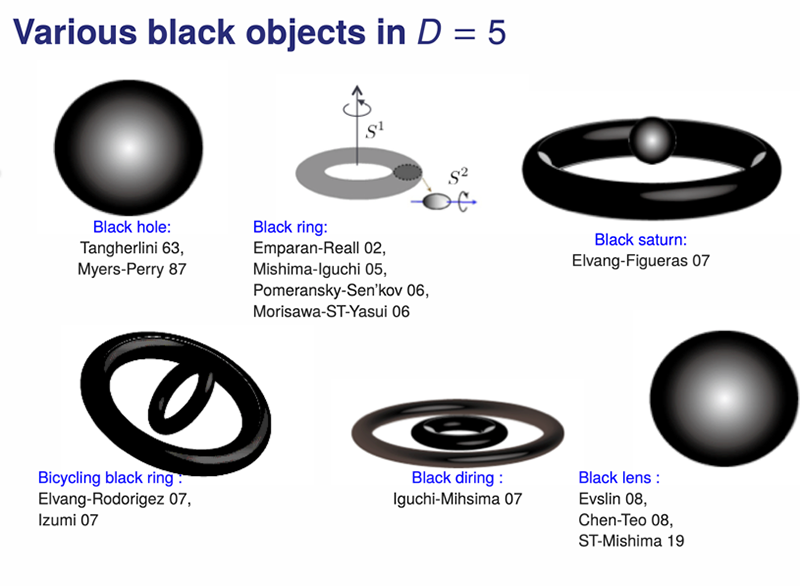
これまでに発見された高次元ブラックホール
